Üçgende Açılar Test-2

TYT-AYT Geometri konuları üçgende açılar test-2 ve çözümleri …

Görselleri inceleyebilir, sayfa sonundan PDF formatındaki 9. Sınıf Üçgende Açılar Test-2 dosyasını bilgisayarınıza indirebilirsiniz.

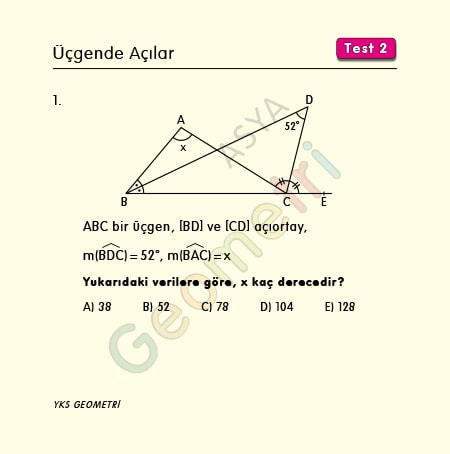
Problem 1 :

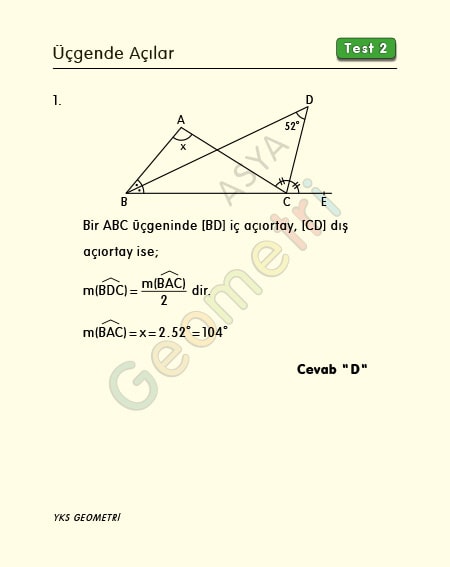
ABC bir üçgen, [BD] ve [CD] açıortay, m(BDC)=52° ise; m(BAC)= x kaç derecedir?

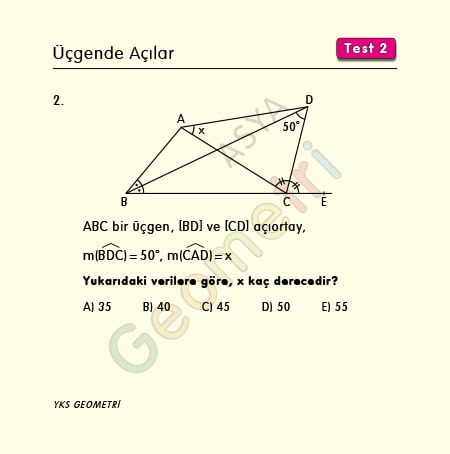
Problem 2 :

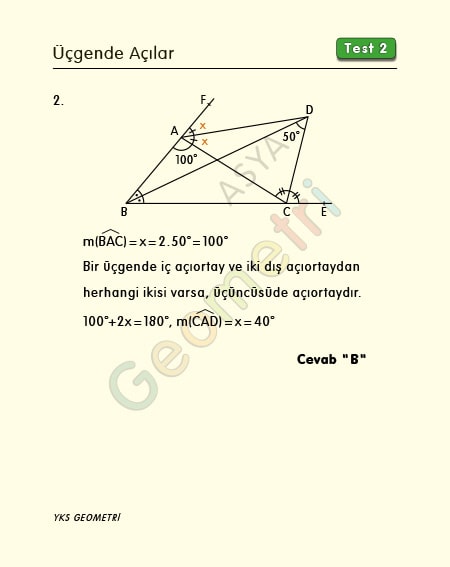
ABC bir üçgen, [BD] ve [CD] açıortay, m(BDC)=50° ise; m(CAD)= x kaç derecedir?

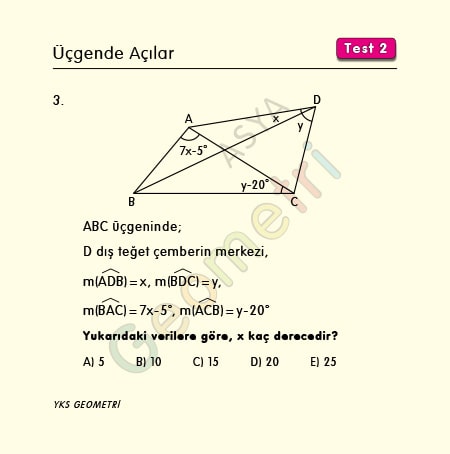
Problem 3 :

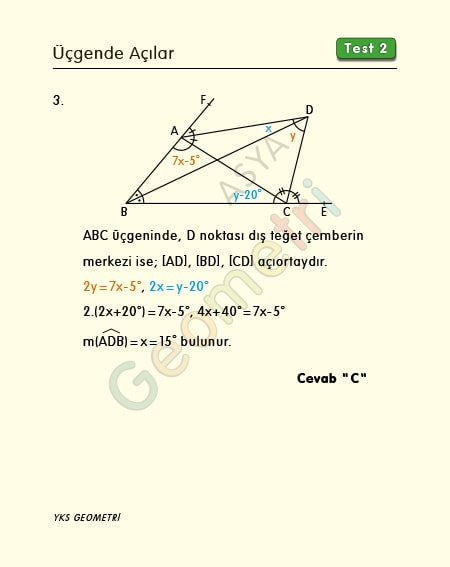
ABC üçgeninde; D dış teğet çemberin merkezi, m(ADB)=x, m(BDC)=y, m(BAC)=7x-5°, m(ACB)=y-20° ise;  x kaç derecedir?

Problem 4 :

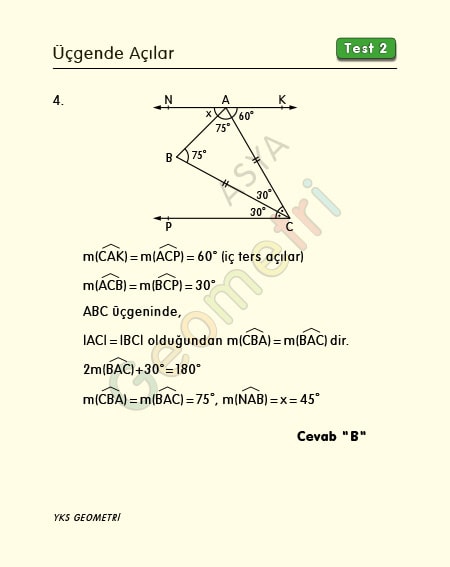
KN // [CP, m(ACB)=m(BCP), |AC|=|BC|, m(CAK)=60° ise; m(NAB)= x kaç derecedir?

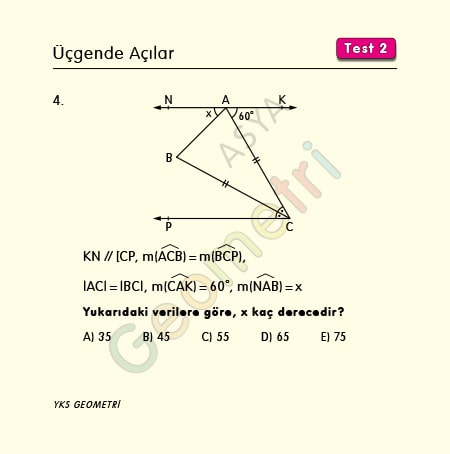
Problem 5 :

[AD // NP, [AC] açıortay, |AB|=|CD|, m(ABN)=2m(PBD) ise; m(DCA)= x kaç derecedir?

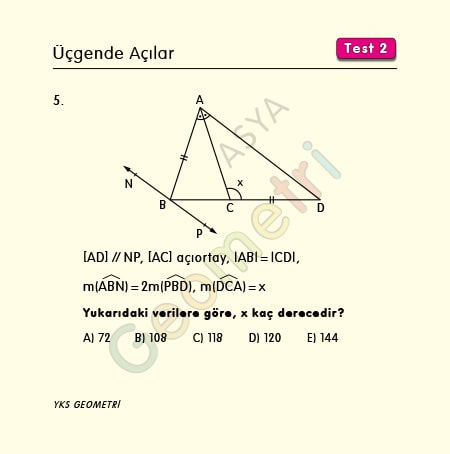
Problem 6 :

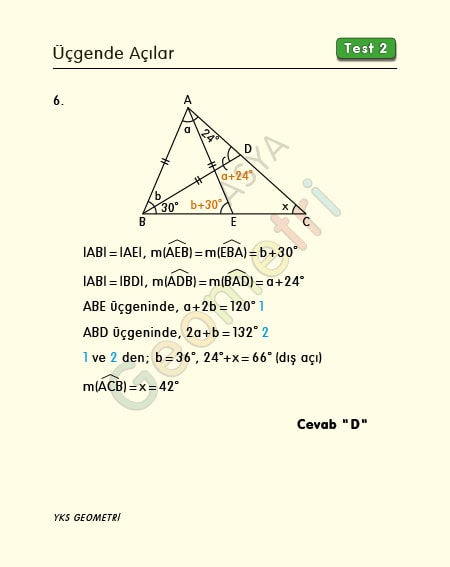
ABC bir üçgen, |AB|=|AE|=|BD|, m(EAC)=24°, m(CBD)=30° ise; m(ACB)= x kaç derecedir?

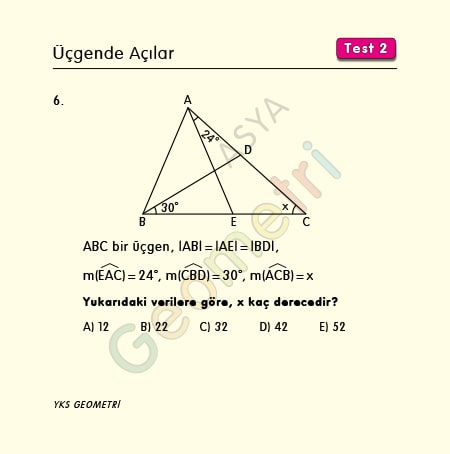
Problem 7 :

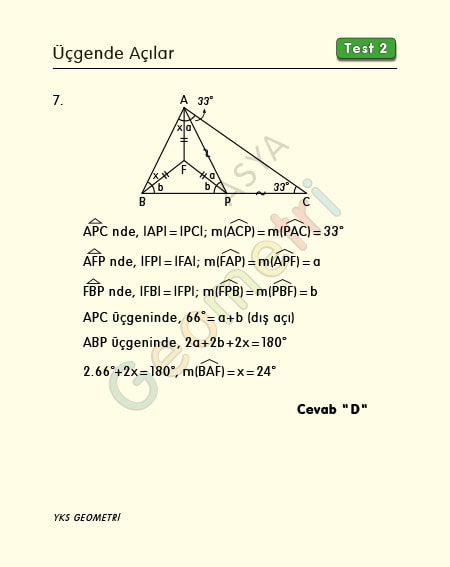
ABC üçgen, |AP|=|PC|, |FA|=|FB|=|FP|, m(ACB)=33° ise; m(BAF)= x kaç derecedir?

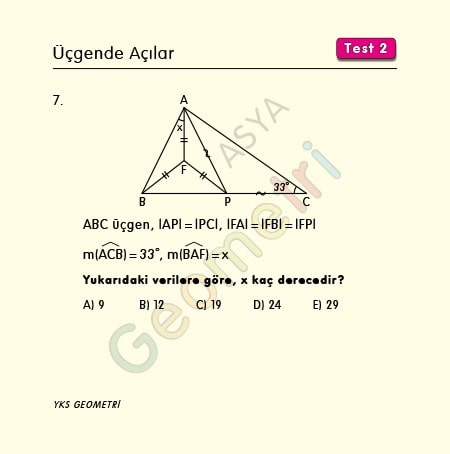
Problem 8 :

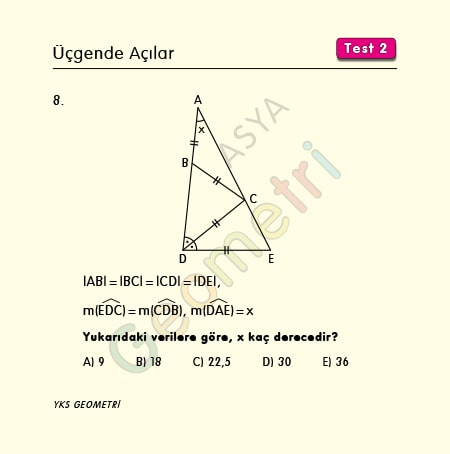
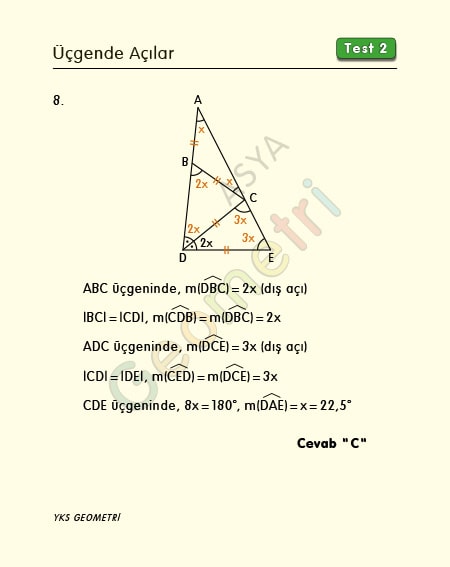
|AB|=|BC|=|CD|=|DE|, m(EDC)=m(CDB) ise; m(DAE)=x kaç derecedir?

Üçgende Açılar Test-2 Çözümleri

Problem 1’in çözümü :

ABC üçgeninin bir iç açıortay ile bir dış açıortayının kesişmesiyle oluşan m(BDC)=52°, m(BAC) açısının yarısı olacağından m(BAC)=2.52°=104° olur.

Problem 2’nin çözümü :

ABC üçgeninin bir iç açıortay ile bir dış açıortayı kesiştiğinden m(BAC)=100° dir. Üçgende iç açıortay ve iki dış açıortaydan herhangi ikisi varsa üçüncüsü de açıortaydır. (D noktası ABC üçgeninin dış teğet çemberinin merkezidir.) Bu durumda m(CAD)=x=40° olur.

Problem 3’ün çözümü :

[AD], [BD], [CD] açıortaydır. ABC üçgeninin; [BD] iç açıortayı ile [CD] dış açıortayından 2y=7x-5°, [BD] iç açıortayı ile [AD] dış açıortayından 2x=y-20° olur. Birinci dereceden iki bilinmeyenli denklem sistemin çözümünden x=15° hesaplanır.

Problem 4’ün çözümü :

İç ters açılardan eş açılar 30’ar derecedir. İkizkenar üçgende m(BAC)=75° olur. Doğru açıdan x=45° bulunur.

Problem 5’in çözümü :

m(BAC)=m(CAD)=a dersek, iç ters açılardan m(ABN)=2a olur. m(ABN)=2a ise m(PBD)=a dır. m(ADB)=a (iç ters açı).|AC|=|CD| olduğundan |AB|=|AC| olur. m(ACB)=2a (dış açı). ABC üçgeninde m(ACB)=m(CBA)=2a dır. O halde 5a=180°, a=36° olur. x=108° bulunur.

Problem 6’nın çözümü :

|AB|=|AE|; m(AEB)=m(EBA)=b+30°, |AB|=|BD|; m(ADB)=m(BAD)=a+24° olur. ABE üçgeninde a+2b=120°, ABD üçgeninde 2a+b=132° dir. İki bilinmeyenli denklem sisteminin çözümünden b=36° olur. x=42° hesaplanır.

Problem 7’nin çözümü :

ABP üçgeninde a+b=66° (dış açı), 2x+2(a+b)=180° olduğundan; 2x=180°-132°, x=24° dir.

Problem 8’in çözümü :

Yukarıdan aşağıya sırasıyla üçgende eş açı, dış açı, üçgende eş açı, açıortaydan eş açı ve üçgende dış açı, eş açı yazılır. Üçgenin iç açıları toplanır x açısı hesaplanır.

Üçgende açılar test-2 PDF

Ders Geometri, ücretsiz olarak indirilebilen Üçgende Açılar Test-2 PDF dosyasını sunar. Matematik alanında önemli bir yere sahip olan geometri dersi, öğrencilerimizin becerilerini güçlendirmek adına oldukça önemlidir. Bundan dolayı Ders Geometri ekibi, öğrencilerin geometri konularındaki yeteneklerini artırmak için özel olarak hazırlanmış testler sunmaktadır. Bu değerli içerik, ücretsiz olarak temin edilebilen PDF formatındadır.

Üçgen Testleri öğrencilere problem çözme becerilerini geliştirme fırsatı sağlamakta olup, özellikle üniversite giriş sınavları TYT ve AYT’ye hazırlanan öğrenciler için büyük bir destektir. Bu kaynak, geometri alanındaki anlayışı pekiştirmek ve sınav hazırlıklarını daha etkili hale getirmek isteyen her öğrencinin başvurabileceği değerli bir rehberdir.