Dik ve Özel Üçgenler Test-5

TYT-AYT Geometri konuları dik ve özel üçgenler test-5 ve çözümleri…

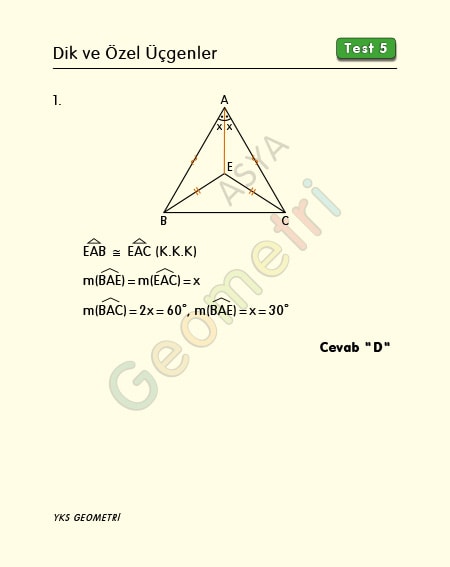
Problem 1 :

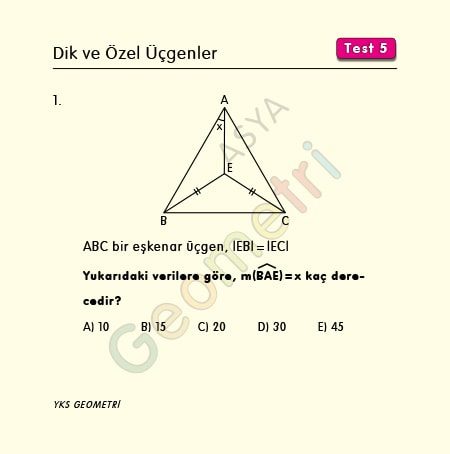
ABC bir eşkenar üçgen, |EB|=|EC| ise; m(BAE)= x kaç derecedir?

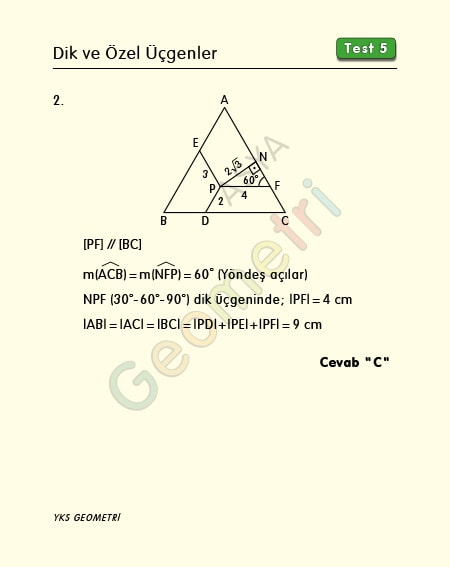
Problem 2 :

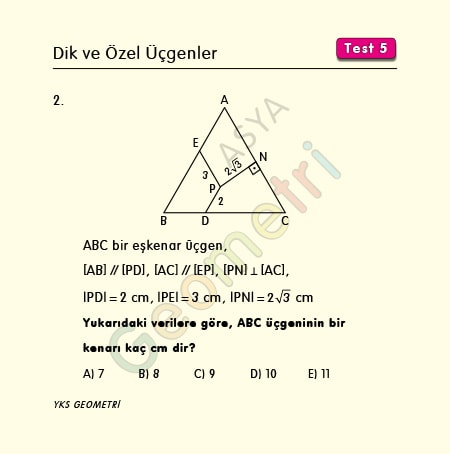
ABC bir eşkenar üçgen, [AB] // [PD], [AC] // [EP], [PN] Ʇ [AC], |PD|=2 cm, |PE|=3 cm, |PN|=2√3 cm ise; ABC üçgeninin bir kenarı kaç cm dir?

Problem 3 :

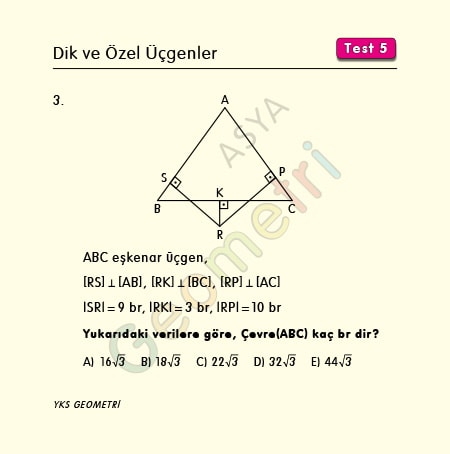
ABC eşkenar üçgen, [RS] Ʇ [AB], [RK] Ʇ [BC], [RP] Ʇ [AC], |SR|=9 br, |RK|=3 br, |RP|=10 br ise; ABC üçgeninin çevresi kaç br dir?

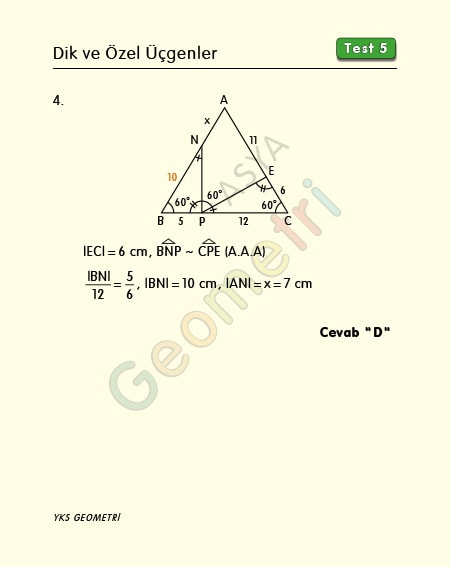
Problem 4 :

ABC bir eşkenar üçgen, m(EPN)=60°, |BP|=5 cm, |PC|=12 cm, |AE|=11 cm ise; |AN|=x kaç cm dir?

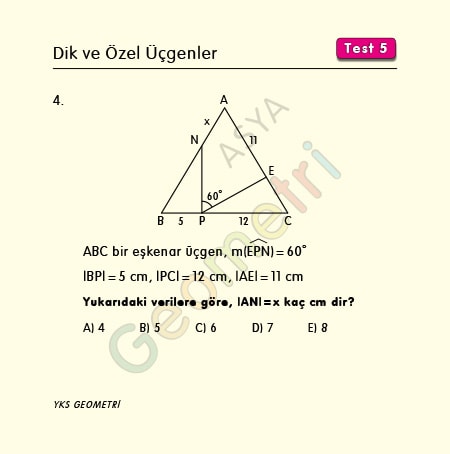
Problem 5 :

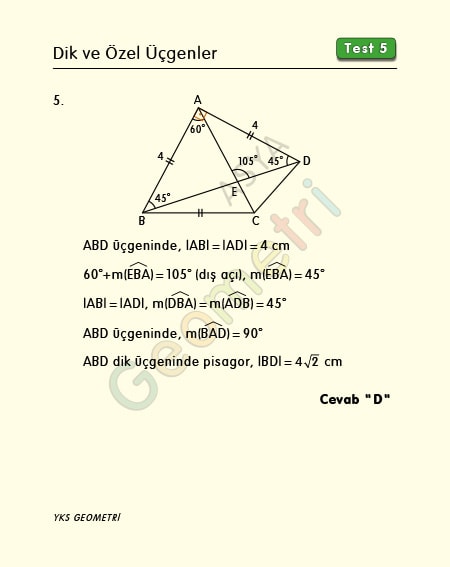
ABC bir eşkenar üçgen, m(DEA)=105°, |BC|=|AD|, |AB|=4 cm ise; |BD| kaç cm dir?

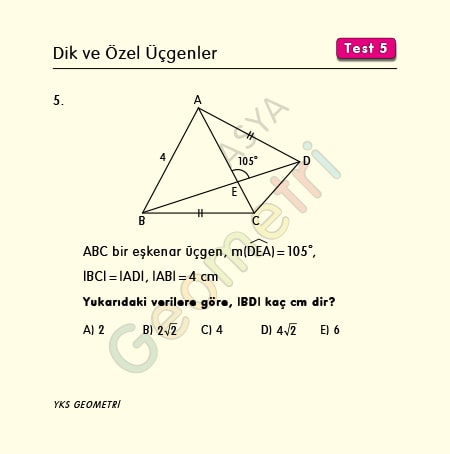
Problem 6 :

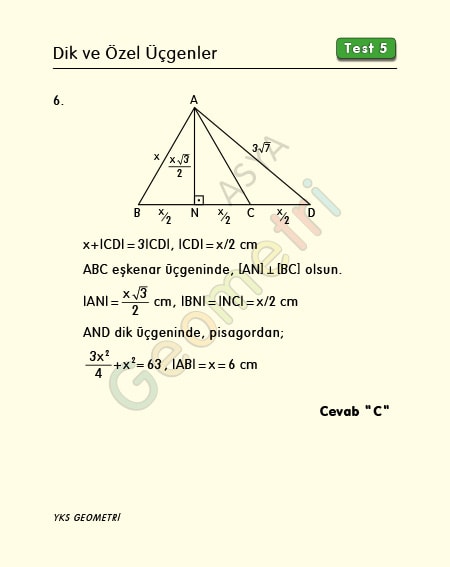
ABC bir eşkenar üçgen, |BD|=3|CD|, |AD|=3√7 cm ise; |AB|=x kaç cm dir?

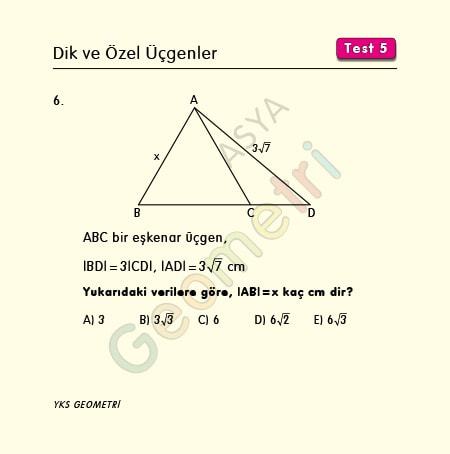
Problem 7 :

ABC ve DBE birer eşkenar üçgen, |DC|=7 cm, |EC|=8 cm ise; |ED| kaç cm dir?

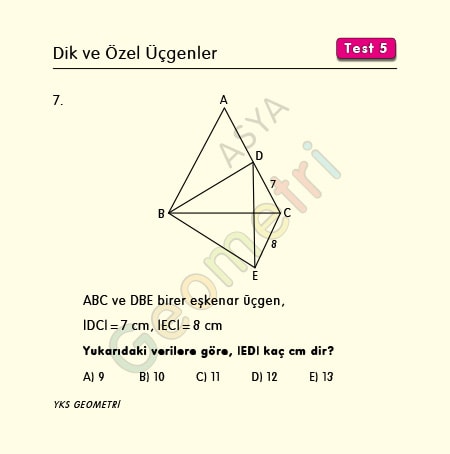
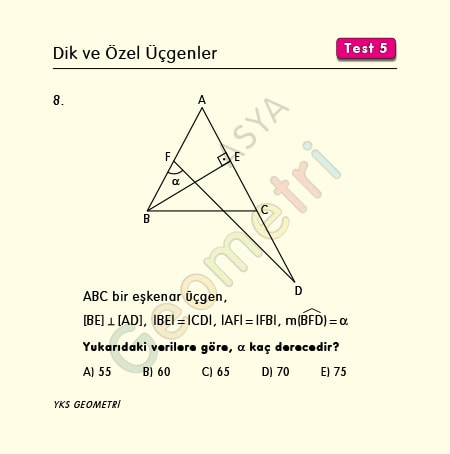
Problem 8 :

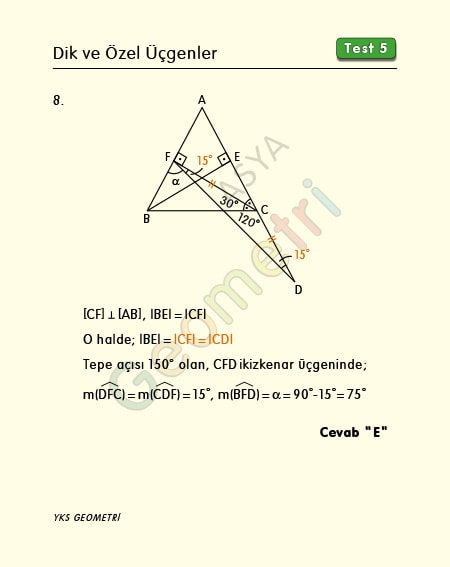
ABC bir eşkenar üçgen, [BE] Ʇ [AD], |BE|=|CD|, |AF|=|FB|, m(BFD)=α ise; α kaç derecedir?

Dik ve Özel Üçgenler Test-5 Çözümleri

Problem 1’in çözümü :

Eşkenar üçgende bulunan üçgenlerin üç kenar uzunluğu eşit olduğundan (K.K.K), üçgenler eştir. Buna göre 2x=60°, x=30° dir.

Problem 2’nin çözümü :

Eşkenar üçgenin içinde alınan herhangi bir noktadan kenarlara çizilen paralellerin toplamı eşkenar üçgenin bir kenarına eşittir. İspatı için geometri soru bankası pdf sayfasına bakınız.

Problem 3’ün çözümü :

Şekildeki ABC eşkenar üçgen sorusu için çıkardığımız formülün ispatını kitabımızda yaptık.

Problem 4’ün çözümü :

|EC|=17-6=11 cm, açılar yerine yazılırsa iki üçgenin A.A.A benzerliğinden x uzunluğu 7 cm bulunur.

Problem 5’in çözümü :

m(EBA)=45°, |BC|=|AD| ve |BC|=|AB| ise |AD|=|AB| olacağından m(ADB)=45° olur. ABD dik üçgeninde dik kenarları 4 cm olduğundan hipotenüs (|BD|) 4√2 cm bulunur.

Problem 6’nın çözümü :

ABC eşkenar üçgeninde yükseklik kenarortaydır. Buna göre |BN|=|NC| dır. |BD|=3|CD| ise |BN|=|NC|=|CD| olur. Dik üçgende pisagor bağıntısından x=6 cm bulunur.

Problem 7’nin çözümü :

İki üçgen eş (K.A.K) olduğundan m(BCE)=60° olur. Üçgenin iki kenarı ve bir açısı bilindiğinden kosinüs teoremini yazalım. x²=7²+8²-2.7.8.cos120 buradan x değeri 13 cm bulunur.

Problem 8’in çözümü :

ABC üçgeninde |AF|=|FB| olduğundan C noktasından AB kenarına çizeceğimiz yükseklik F noktasında diktir. Eşkenar üçgende yükseklikler eşittir. Buna göre |BE|=|CF| dir. O halde |CF|=|CD| olur. Tepe açısı 150 derece olan ikizkenar üçgende taban açıları 15° olacağından alfa açısının ölçüsü 90°-15°=75° bulunur.

Dik ve Özel Üçgenler test-5 PDF

Ders Geometri, ücretsiz olarak indirilebilen PDF formatında Dik ve Özel Üçgenler Test-1 PDF dosyasını sunar. Matematik alanında önemli bir yere sahip olan geometri dersi, öğrencilerimizin becerilerini güçlendirmek adına oldukça önemlidir. Bundan dolayı Ders Geometri ekibi, öğrencilerin geometri konularındaki yeteneklerini artırmak için özel olarak hazırlanmış testler sunmaktadır. Bu değerli içerik, ücretsiz olarak temin edilebilen PDF formatındadır.

Üçgen Testleri öğrencilere problem çözme becerilerini geliştirme fırsatı sağlamakta olup, özellikle üniversite giriş sınavları TYT ve AYT’ye hazırlanan öğrenciler için büyük bir destektir. Bu kaynak, geometri alanındaki anlayışı pekiştirmek ve sınav hazırlıklarını daha etkili hale getirmek isteyen her öğrencinin başvurabileceği değerli bir rehberdir.